Introduction

Figure: “This is not white noise.” Rene Magritte’s 2 cents on time series residual checks (see MagrittePipe).
I am sure you have seen many of those residual check figures in text books, papers, etc. and also have produced them yourselves. However, these plots are misleading because they do not necessarily mean that the series is indeed white noise; in fact, it just shows you that on average it is white noise.
What does that mean? Well, what actually happens is that sample estimates of the autocorrelation function (ACF) 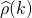 from the entire sequences
from the entire sequences  converge to the temporal average of a possibly time-varying correlation structure
converge to the temporal average of a possibly time-varying correlation structure 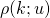 , where
, where ![Rendered by QuickLaTeX.com u = t/T \in [0,1]](http://www.gmge.org/wp/wp-content/ql-cache/quicklatex.com-5053eb58ddc326a1a24ca759203941d7_l3.png) is time rescaled (from
is time rescaled (from ![Rendered by QuickLaTeX.com [0, T]](http://www.gmge.org/wp/wp-content/ql-cache/quicklatex.com-1b423ddb4cea2e2c7624a19269868604_l3.png) ) to the unit-interval.
) to the unit-interval.
This means that when you fit a model, plot the sample ACF of the residuals and all lags 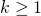 are below the significance line, this just shows that your model can remove auto-correlation on average, but you still have to check if your data has time varying dynamics.
are below the significance line, this just shows that your model can remove auto-correlation on average, but you still have to check if your data has time varying dynamics.
Testing for white noise and proposal for a new white noise test
Why does that matter in practice? Well, it is spurious in the sense that the sample autocorrelation function (ACF) 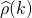 tends to the the ACF of white noise,
tends to the the ACF of white noise, 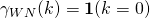 , for
, for 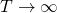 . This means for a large enough sample the sample ACF is indistinguishable from white noise. This is bad!! Especially if we use Portmanteau style white noise tests like the Box-Ljung test.
. This means for a large enough sample the sample ACF is indistinguishable from white noise. This is bad!! Especially if we use Portmanteau style white noise tests like the Box-Ljung test.
Box.test(yy, lag = 5, type = "Ljung-Box")
##
## Box-Ljung test
##
## data: yy
## X-squared = 5.5603, df = 5, p-value = 0.3514
Using the popular white noise test we wouldn’t reject white noise (p-value: 0.3513767) – even though we know it is not white noise. This shows you that the Ljung-Box test has very low power against locally stationary alternatives.
In the paper I propose a simple windowing approach to improve the power against such locally stationary alternatives – locally stationary Lung Box test.
Box.test.ls(yy, lag = 5, K = 2, type = "Ljung-Box")
##
## LS Ljung-Box test; Number of windows = 2; non-overlapping window
## size = 500
##
## data: yy
## X-squared = 47.813, df = 10, p-value = 6.715e-07
Here even with already two windows (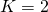 ) we can detect the non-stationarity.
) we can detect the non-stationarity.
See the paper for details and from now on beware when someone shows you an ACF plot with a Ljung-Box test to justify that their models produce white noise residuals.
Note: I do note that the locally stationary deviation from white noise might not always be important for the application at hand. However, in principle to understand the dynamics of the process – and to get even better forecasts – you should care about it.
Update: It is true that this might look just like a theoretically interesting case, but not seen in practice. I agree it is unlikely to see such spurious white noise in a real world dataset directly, but you will see this in almost any residuals of a stationnary model. Without going into too much theoretical detail, just imagine a general time-varying model 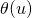 with a time varying covariance function
with a time varying covariance function 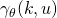 . Well if you fit a constant model to this with parameter
. Well if you fit a constant model to this with parameter 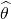 then this estimate will be close to the time average of the true model
then this estimate will be close to the time average of the true model 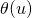 ; and naturally the residuals will now be close to
; and naturally the residuals will now be close to 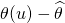 which by construction of
which by construction of 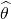 will integrate out to zero (approximately).
will integrate out to zero (approximately).
Let’s look at an example
library(fracdiff)
library(data.table)
tree.ring <- ts(fread(file.path(data.path, "tree-rings.txt"))[, V1])
layout(matrix(1:4, ncol = 2))
plot(tree.ring)
acf(tree.ring)
mod.arfima <- fracdiff(tree.ring)
mod.arfima![Rendered by QuickLaTeX.com d ## [1] 0.236507 arfima.res <- diffseries(tree.ring, mod.arfima](http://www.gmge.org/wp/wp-content/ql-cache/quicklatex.com-7b61d8eba280e90666cd096c05b43cd0_l3.png) d)
plot(arfima.res)
acf(arfima.res)
d)
plot(arfima.res)
acf(arfima.res)

Looks good right? Well, the issue is that the residuals are spurious white noise. How do I know? First, I can test it
Box.test(arfima.res, type = "Ljung-Box")
##
## Box-Ljung test
##
## data: arfima.res
## X-squared = 1.8757, df = 1, p-value = 0.1708
Box.test.ls(arfima.res, K = 4, type = "Ljung-Box")
##
## LS Ljung-Box test; Number of windows = 4; non-overlapping window
## size = 497
##
## data: arfima.res
## X-squared = 39.361, df = 4, p-value = 5.867e-08
and second, we know from literature that the tree ring data is in fact locally stationary fractional noise: see Goerg (2012) and Ferreira, Olea, and Palma (2013).
Appendix
Code
Simulating a locally stationary 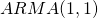 process:
process:
lsarma11.sim
function (n, phi = 0, theta = 0, sigma = 1, rand.gen = rnorm,
innov = rand.gen(n))
{
u.d <- seq_len(n)/n
phi.u <- as.function(polynomial(phi))
theta.u <- as.function(polynomial(theta))
phi.t <- phi.u(u.d)
theta.t <- theta.u(u.d)
if (sigma == "constant") {
var.arma11 <- (1 + theta.t^2 - 2 * theta.t * phi.t)/(1 -
phi.t^2)
sigma.t <- sqrt(1/var.arma11)
}
else {
sigma.u <- as.function(polynomial(sigma))
sigma.t <- sigma.u(u.d)
}
xx <- innov
for (ii in 2:n) {
xx[ii] <- phi.t[ii] * xx[ii - 1] + sigma.t[ii] * innov[ii] +
theta.t[ii - 1] * sigma.t[ii - 1] * innov[ii - 1]
}
return(ts(xx))
}
The locally stationary Box test:
Box.test.ls
function (x, lag = 1, type = c("Ljung-Box", "Box-Pierce"), fitdf = 0,
K = 1, plot = FALSE, ...)
{
stopifnot(is.numeric(x), K >= 1, K == round(K), is.logical(plot))
type <- match.arg(type)
if (K >= length(x)) {
stop("Number of windows must be smaller than the length of the time series.")
}
N.k <- floor(length(x)/K)
if (K == 1) {
Box.test(x, type, lag = lag)
}
else {
METHOD <- paste0("LS ", type, " test; \n Number of windows = ",
K, "; non-overlapping window size = ", N.k)
stats.pvals <- rollapply(yy, width = N.k, by = N.k, FUN = function(x) {
out <- Box.test(x, lag = lag, type)
return(c(out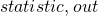 p.value))
}, fill = NA)
stats.pvals <- stats.pvals[!is.na(stats.pvals[, 1]),
]
colnames(stats.pvals) <- c("statistic", "p-value")
if (plot) {
plot(stats.pvals[, "p-value"], ylim = c(0, max(stats.pvals[,
"p-value"])), type = "h", lwd = 2, ylab = "p-value",
xlab = "Window")
abline(0.05, 0, col = 4, lty = 4)
abline(0, 0, lty = 1, col = "gray")
}
STATISTIC <- sum(stats.pvals[, "statistic"])
names(STATISTIC) <- "X-squared"
df.total <- lag * K
names(df.total) <- "df"
PVAL <- 1 - pchisq(STATISTIC, df.total)
return(structure(list(statistic = STATISTIC, parameter = df.total,
p.value = PVAL, method = METHOD, data.name = deparse(substitute(x))),
class = "htest"))
}
}
p.value))
}, fill = NA)
stats.pvals <- stats.pvals[!is.na(stats.pvals[, 1]),
]
colnames(stats.pvals) <- c("statistic", "p-value")
if (plot) {
plot(stats.pvals[, "p-value"], ylim = c(0, max(stats.pvals[,
"p-value"])), type = "h", lwd = 2, ylab = "p-value",
xlab = "Window")
abline(0.05, 0, col = 4, lty = 4)
abline(0, 0, lty = 1, col = "gray")
}
STATISTIC <- sum(stats.pvals[, "statistic"])
names(STATISTIC) <- "X-squared"
df.total <- lag * K
names(df.total) <- "df"
PVAL <- 1 - pchisq(STATISTIC, df.total)
return(structure(list(statistic = STATISTIC, parameter = df.total,
p.value = PVAL, method = METHOD, data.name = deparse(substitute(x))),
class = "htest"))
}
}